Binomial Theorem for Expansion Worksheets
There will be times when you are looking at binomials that you must further simplify or evaluate, and they confuse you because they seem endless. This is especially true when you have a complex exponent to work with as part of the expression. This is where this theorem can be used as tool to reform the expression and help you speed up your day. This series of worksheets and lessons has students learn a quick way to expand binomial expressions with the help of the Binomial Theorem. Make special note of this tool because as you advance, you may forget that it is in your toolbox.
Aligned Standard: HSA-APR.C.5
- Expand the Binomial Step-by-step Lesson- We introduce you to the Binomial Theorem.
- Guided Lesson - Run wild with expanding these three binomials. See how they line up with the formula.
- Guided Lesson Explanation - I start by explaining the basic procedure for solving such problems.
- Practice Worksheet - A series of problems that will have you completely understanding the concept end to end.
- Matching Worksheet - Match the binomials to their expand form. You will just need to expand all of them out.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
This is another skill that I didn't see coming when the Common Core was presented.
- Homework 1 - Binomial expressions contain two terms. The first terms is seen as an and the last term is seen as bn. When binomial expressions are raised to a power, they can be expanded using the following expansion formulas.
- Homework 2 - In this case, the binomial is raised to the third power, so we will use this formula raised to it as well.
- Homework 3 - We complete these problems by simply inserting the values into the formula.
Practice Worksheets
In the past, the theorem was always given to you. You find the theorem in most engineering field manuals.
- Practice 1 - Start to get some practice with this skill up on the next level.
- Practice 2 - Why would you go any further with that one? They are pulled apart pretty well.
- Practice 3 - Expand the expression using the Binomial Theorem.
Math Skill Quizzes
Expanding beyond the fourth power is much more difficult for kids at this level.
- Quiz 1 - Take it a few steps further. This will help you use algebra to solve some pretty complex problems.
- Quiz 2 - This is a very fair choice of problems that can be done quickly.
- Quiz 3 - A nice quiz for review to help you gauge how well you know this stuff.
What is the Binomial Theorem for Expansion?

Ever come across very long algebra problems and got stuck? Well, this is where the binomial theorem comes in for the rescue. A lot of people are skeptical about using the theorem as it looks very complicated, but people who get used to it say that there is nothing simpler and easier than a binomial expansion to solve a horrendously long algebra problem. It helps us expand expressions that follow the form (a + b)n. It demonstrates the result of multiplying a binomial by itself repeatedly as many times as you want. For example, if we wanted to find out the end value of the expression (3x + y)5, the Binomial Theorem for Expansion would provide us a shortcut for getting this done.
There are going to be times in your life where you will come across very complex and overstated algebra problems. When you have a binomial that you would like to expand you can use Pascal’s Triangle to make your life a little easier for a few minutes. You will run into this whenever you need to repeatedly multiply a binomial by itself. This happens when you have an exponential binomial. Using the binomial theorem is intuitive. Once you get a hang of it, it is not too hard to use this method of expansion. At first look it truly is one of the most intimidating equations you will encounter. Take a look at the lesson below and you will see what I mean.
As far as using the theorem, it tells us that we expand an expression with power in form of (y + y)n into a sum involving the terms of the form axbyc. It should be stated that both of the exponents (b and c) in this form must non-negative with b + c = n. The coefficient a is a positive integer as well. If the exponent were to be zero, the theorem states that some terms will be omitted and you will be left with 3x< sup>2.
How Do You Process This Calculation?
Like we said before, this theorem immediately will overwhelm you. Just look at this scary thing:
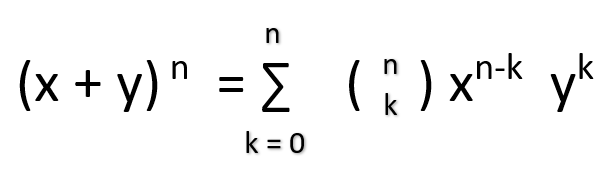
If we look to the left of the equals symbol this just says that when you have a binomial expression (x + y) that is being raised to a power (n). If the y value is a negative constant, it is important to remember that it is a negative value so that you can translate that into the expression on the right side of the equation. We then just substitute the values of the variables (x, y, and n) into their respective place on the right-hand portion of the equation. Looking at the right side of the equation after we have substituted the values leaves us with two things left unanswered. The sigma notation just tells us that we’ll be adding many (n) variables together. The n choose k combination helps you determine the number of different ways you could choose k elements. Once you complete a few of these problems you quickly learn that this is much easier than it looks.