Addition of Numbers (Under 100)
How to Add Single and Double-Digit Numbers? Adding single- and double-digit numbers is the higher stage of learning numbers. A lot of young minds are unable to grasp the concept and can lag behind their friends. Here are some easy ways of adding single-and double-digit numbers. Adding Single Digit Numbers There are two methods of adding single-digit numbers. Method 1: Counting - Pick the first number of the sum, and this will be where your counting will begin. Count up from the starting number by the number of places as the second number of the sum. Method 2: Using Number Line - Make a number line from 1 till 9. Locate the first number of the sum on the number line and move places equal to the second single-digit number. The number at which the pencil stops will be the answer to the sum. Adding Double-Digit Numbers - Adding double-digit numbers can be complex. By following these rules, you can easily sole two-digital sums. Start from the Right Side- Start solving the sum from the right side. Sum the numbers on the right-hand side first and proceed from right to the left side of the sum. Carry the to the Left Side -When the sum of the numbers on the right-side is a two-digit number, write the righthand digit below the numbers on the right side, carry the left-hand digit to the left side of the equation. Now add the two numbers on the left side of the equation and the carried digit. These worksheets workthrough adding single and double digits together to top out at triple digit sum.
Aligned Standard: Grade 1 Numbers - 1.NBT.4
- Sums to 100 Step-by-step Lesson- This is a 3 part lesson. Double and single digit sums, Two Digits and Multiple of 10s sums, and straight double digit sums.
- Horizontal, Vertical, a Picture Sums Guided Lesson - Working on the same skills in the lesson, but we add pictures to the mix. Everything works in rows and is monitored for you.
- Guided Lesson Explanation - I use a general explanation here. See if you think it is clear enough for students. We set everything up vertically.
- Adding Double Digits Practice Worksheet - 10 problems setup in a vertical fashion. The format is easy to follow.
- Horizontal Matching Worksheet - This is another great lead into algebra skills at this level. Missing numbers is always the move.
- Answer Keys - These are for all the unlocked materials above.
- Guided Lesson 1 - We work on the horizontal sum of two double digit numbers. Add both the number in the tens place and write the total of the sum.
- Guided Lesson 2 - Much of the same, but we tangle with zeroes now.
- Guided Lesson 3 - We go all vertical on you.
- Guided 4 - The sum of sixes at the ones place throws more kids than you would think.
- Picture Explanation - A simple refresher for anyone who is struggling with this.
- Compare Numbers Worksheet - This one is good to throw in there for more repetition.
- Addition of Numbers Matching Worksheet - We baby step our way to sums over 100.
- Solving Sums (under 100) Table Worksheet - The box is filled with sums. Find their solution.
- Visually Adding Objects Worksheet - Which sum matches the egg problems?
Guided Lessons
Place values are great to cover before stepping up to higher levels with sums.
Practice Worksheets
I went in a lot of different directions with these to help teachers and students see different angles.
Example of Adding Single- and Double-Digit Numbers:
This problem asks you to find the sum between 77 and 6. If you look to the problem setup to the right, we align the 6 with the ones place of the 77.
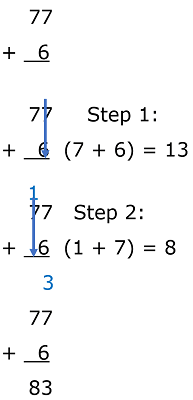
Solution: Step 1) Add the values of the ones column. You will see that the blue arrow indicates what we are adding and the value 7 + 6 is displayed. When we add these two integers, the sum is 13.
Begin with the setup: We place the sum (13) that we previously found in alignment with the problem setup. The 3 from the ones column gets dropped into the answer column at the bottom. The 1 from the tens column gets placed above the 7 (that represented 70).
Step 2) All that is remaining to find the sum of is the tens column which is (1 + 7) or 8. We then just place this value (8) in the tens column. So our final answer is: 77 +6 = 83.
Example of Adding Double-Digit Numbers:
This example builds from the skill that you just reviewed above. The set up and process is terribly similar. It all comes down to how you align the problems. This problem asks you to find the sum of 39 and 25. If you look to the problem setup to the right, we align both of their place values (ones and tens) in a vertical alignment. This helps us to see how the values directly relate to one another.

Solution: Step 1) Add the values of the ones column. You will see that the blue arrow indicates what we are adding and the value 9 + 5 is displayed. When we add these two integers, the sum is 14.
Begin with the setup: We place the sum (14) that we previously found in alignment with the problem setup. The 4 from the ones column gets dropped into the answer column at the bottom. The 1 from the tens column gets placed above the both the 3 (that represents 30) and the 2 (that represents 20).
Step 2) All that is remaining to find the sum of is the tens column which is (1 + 3 + 2) or 6. This 6 represents 60, so we place this value (6) in the tens column. So, our final answer is: 39 + 25 = 64.